C# 7.0 introduced the new feature of ref return and ref locals. I have to say, I wasn't sure about the actual usefulness of the feature, but with the recent additions of reference semantics with value types in C# 7.2 I do see how they can be useful, even if only in a niche section of the industry.

So I was talking about these new features at one of my workshops and of course my intro example was something like the one that's on docs.microsoft.com for the ref return:

class Program
{
  static ref int FindNumber(int target, int[] numbers)
  {
    for (int i = 0; i < numbers.Length; i++)
    {
      if (numbers[i] == target)
         return ref numbers[i];
    }
    throw new ArgumentException("Cannot find target");
  }

  static void Main(string[] args)
  {
    int[] values = new[] { 1, 2, 3, 4, 5, 6 };
    ref int result = ref FindNumber(3, values);
    result = 19;
    Console.WriteLine(values[2]); // What does this print?
    Console.ReadLine();
  }
}

Using ref returns and ref locals, this will of course print 19 to the console. That's the whole point of ref returns and ref locals.

And then I got the question from someone in the audience: what happens when the array is not a method a parameter, but instead a local variable in FindNumber? Usually, the when a method is done executing the local variables of the method are "destroyed". If the local variables are value types, then their allocated space in the stack are automatically freed, if they are reference types, then the reference itself is destroyed and sometime later comes the GC and cleans up the heap space that the local variable referred to.

Arrays are reference types so they belong to the latter category. But what happens if an element of the local array is returned by reference? Does this mean that the whole array is kept in the memory?

Short answer: yes. If you return an element of the array by reference, then this creates a new reference to the array and this reference "gets out" of the method as the return value (remember, this s the reference-return case), so the whole array is kept in the memory, even though the array itself and the other element cannot be accessed any more — thus creating a memory leak in a managed programming environemnt. Nice job :)

Long answer: to validate what happens, we can write a little program:

class Program
{
  static ref int FindNumber(int target)
  {
    int[] numbers = new[] { 1, 2, 3, 4, 5, 6 };
    Console.WriteLine("Array allocated...");
    Console.ReadLine();
    for (int ctr = 0; ctr < numbers.Length; ctr++)
    {
      if (numbers[ctr] == target)
        return ref numbers[ctr];
    }
    throw new ArgumentException("Cannot find target");
  }

  static void Main(string[] args)
  {
    ref int result = ref FindNumber(3);
    Console.WriteLine("Method done, running GC and modifying element");
    GC.Collect();
    GC.WaitForPendingFinalizers();
    GC.Collect();
    result = 19;
    Console.WriteLine("GC done");
    Console.ReadLine();
    // this is just in case something wants to optimize away the whole local
    Console.WriteLine(result);
  }
}

So here, the method creates an array. At this point, we'll use WinDbg to get the address of the array and dump the contents. Then the method runs as it should and exits and control is returned to the Main method. In the Main method garbage collection is forced and the array element is modified. After the GC is done, we can query the address again to see if the array still exists; if it does, it is a pretty strong (though not definitive) indication that the array is kept and not garbage collected.

So let's fire up WinDbg and open the exe (built in release mode of course). I just use the g command to let the program run until the first message appears on screen. When the first message appears and Console.ReadLine() blocks the execution, I break in WinDbg (using CTRL+break) and load the SOS extension using:

.loadby sos clr

After that I dump the heap using !dumpheap and look for my integer array. You can just click on the list of int arrays in the output of the command and then click on Address for each array.

The output shows you the length (rank) of the array. If you find one that has 6 elements, then it's possibly the local array. To validate run the command:

!DumpArray -details 04eb2478

Where the last parameter is the array of the address. The output lists you the elements in the array:

When you found your array, keep the command at hand and let the code continue by issuing the g command again.

After the second message appears on the console, the control is in the Main() method and by that time, the GC should have collected all the memory garbage (including the array) and the element should have been modified. So let's break the execution again, and issue the same command for dumping the array as before. And if everything's been done right, you can see that the array still exists at the same address, and you can even see that the element has been modified:

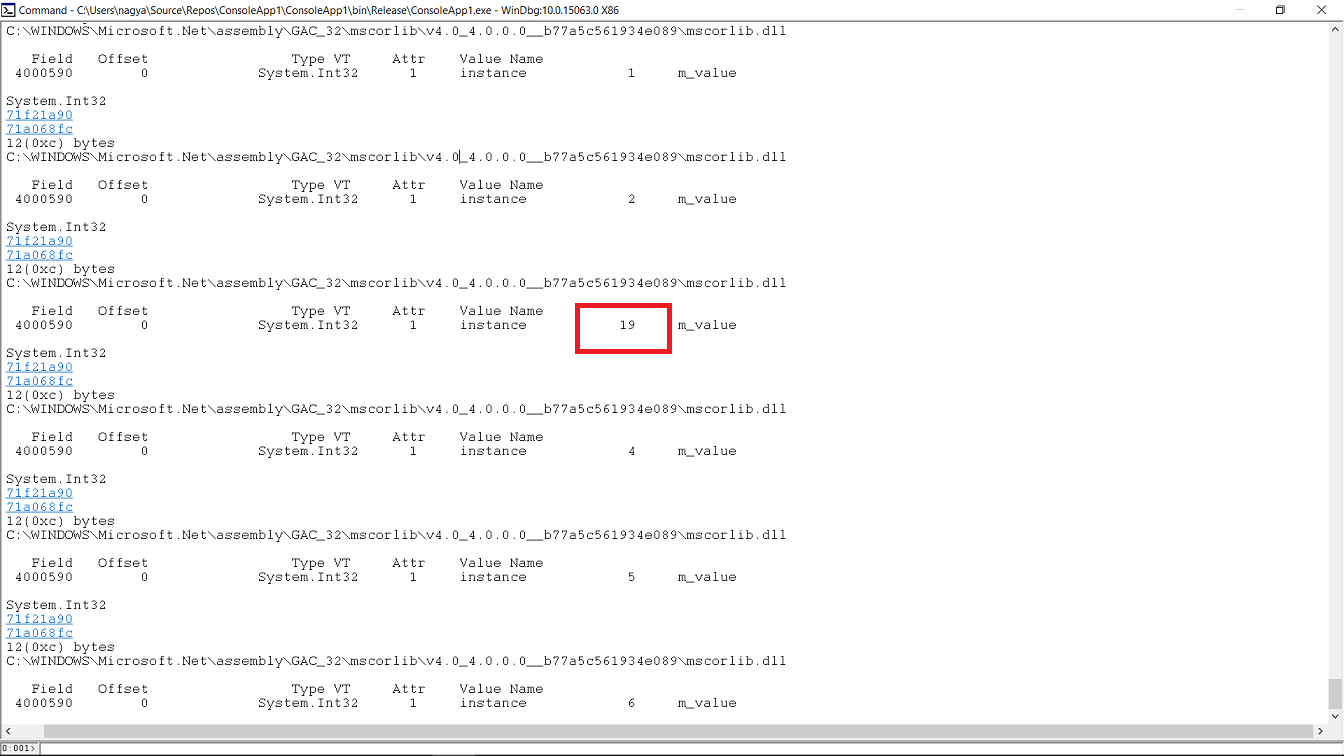
So, there's proof that probably the array is kept in the memory through the reference created by the ref return. You can run the same experiment by modifying the FindNumber() method not to be ref return. In that case you'll see that the array cannot be dumped from its original address in the Main() method after the GC has run. (You'll probably get something like 'Not an array, please use !DumpObj instead' and if you try !DumpObj <address>, you'll get 'Free object' as the result, showing you that the array indeed has been freed).

Conclusion: be careful when you use ref returns.